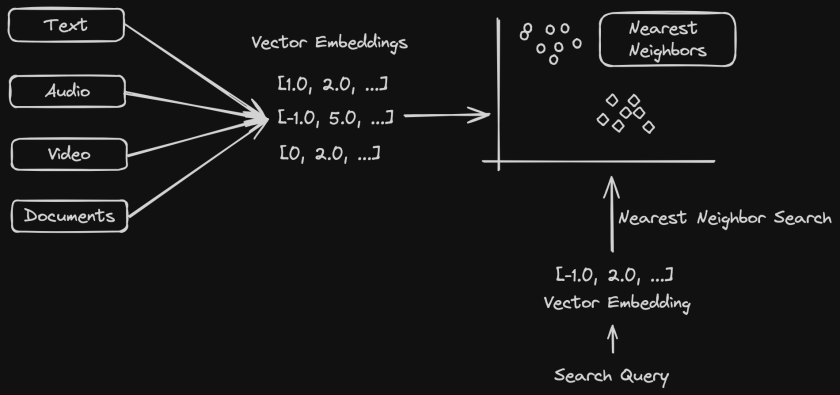
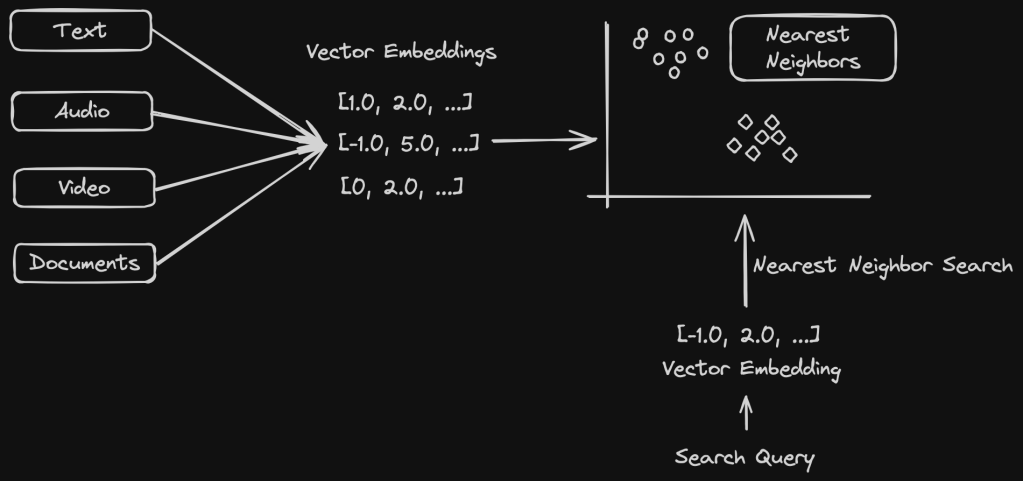
We learnt about Semantic Search in my previous post. Here is the link if you missed it. K-Nearest Neighbors is one of the most popular Machine Learning algorithms used in semantic search to find documents or data that is semantically similar to a user’s query.
To recap, documents are represented as vector embeddings in a vector space model that captures semantic similarities based on the context. A user query is then converted to a vector embedding and efficient algorithms such as KNN, ANN (Approximate Nearest Neighbor) search are used to find the nearest neighbors to the query. This is where K-Nearest Neighbors algorithm is used where “K” refers to the number of nearest neighbors we want to consider before prediction.

How does KNN work?
KNN works by finding the “K” nearest neighbors in a vector space model. The value of K needs to be chosen carefully to balance between noise and over smoothing. One way is to test for accuracy of the algorithm by evaluating on different values of K using cross-validation where data is divided into training and validation datasets. The validation data set is used to evaluate the performance of the algorithm. A plot with K values and the corresponding error rate can help determine the best K value with the minimum error rate.
KNN finds the nearest neighbors using distance metrics. This can be anything such as Euclidean distance, Manhattan distance etc. We will look at the various distance metrics in detail in the next section.
KNN can be used for both Classification and Regression problems.
- For Classification problems, the majority class is chosen among the K nearest neighbors.
- For Regression problems, the average (or the weighted average) of the K nearest neighbors is used.
Distance Metrics
Various distance metrics are used for KNN, Euclidean distance being one of the most common ones.
Euclidean Distance

Euclidean Distance gives the straight line distance between two coordinates in a vector space. This works great for numerical features in the input data.
Manhattan Distance

Manhattan Distance calculates the sum of absolute differences between the vector data points. This is good with categorical features. It is not as sensitive to outliers as Euclidean Distance.
Mikowski Distance

Mikowski Distance is a generalization of the above distances.
- If p = 1, we get Manhattan Distance
- If p = 2, we get Euclidean Distance
Hamming Distance
Hamming Distance between two vectors of same length is the number of positions where the corresponding vector values are different. This is suitable for categorical and even binary data.
Cosine Similarity

This is commonly used for high dimensional vector data or text data and it calculates the distance using the cosine of the angle between two vectors.
KNN Algorithm Example for Classification
We have a good understanding of KNN. Now let us look at an actual code example of KNN for a Classification problem.
As a coding exercise, try to implement the averaging functionality for a regression KNN algorithm on your own.
from algorithms.knn import distances
METRICS = {
"euclidean": distances.EuclideanDistance(),
"manhattan": distances.ManhattanDistance(),
"mikowski": distances.MikowskiDistance(),
"hamming": distances.HammingDistance(),
"jaccard": distances.JaccardDistance(),
"cosine": distances.CosineDistance()
}
def get_majority_element(computed_distances):
"""
Takes an iterable of tuples (distance, class_type)
and finds the majority class_type
:param computed_distances: iterable of tuples
:return: majority element: string
"""
freq = {}
for _, class_type in computed_distances:
if class_type not in freq:
freq[class_type] = 1
else:
freq[class_type] += 1
return max(freq, key=freq.get)
def knn(training_data, k, distance_metric, test_value):
"""
Find the k nearest neighbors in training_data for the
given test value to determine the class type
:param training_data: Dictionary of class type keys and list of vectors
as values
:param k: Integer
:param distance_metric: string
:param test_value: query vector
:return:
"""
if distance_metric not in METRICS:
raise ValueError(distance_metric + "is not a valid input")
distance_calculator = METRICS[distance_metric]
computed_distances = []
for class_type, points in training_data.items():
for point in points:
distance = distance_calculator.calculate(point, test_value)
computed_distances.append((distance, class_type))
# sort the tuples by the computed distance
computed_distances.sort()
return get_majority_element(computed_distances[:k])
from abc import abstractmethod, ABC
from math import pow, sqrt
ROUND_TO_DECIMAL_DIGITS = 4
class Distances(ABC):
@abstractmethod
def calculate(self, x1, x2):
pass
class EuclideanDistance(Distances):
def calculate(self, x1, x2):
"""
Compute the Euclidean distance between two points.
Parameters:
x1 (iterable): First set of coordinates.
x2 (iterable): Second set of coordinates.
Returns:
float: Euclidean Distance
"""
if len(x1) != len(x2):
raise TypeError("The dimensions of two iterables x1 and x2 should match")
return round(sqrt(sum(pow(p1 - p2, 2) for p1, p2 in zip(x1, x2))), ROUND_TO_DECIMAL_DIGITS)
Real World Applications of KNN
KNN is used in a variety of applications such as
- Recommendation Systems – to recommend the most popular choices among users for collaborative filtering by identifying users with similar behavior.
- Disease Classification – it can predict the likelihood of certain conditions using majority voting.
- Semantic Search – to find semantically similar documents or items for a user’s query.
- Text Classification – spam detection is a good example.
- Anomaly Detection – It can signify data points that differ from the rest of the data in a system and many many more.
I hope you enjoyed reading about K-Nearest Neighbors algorithm. We will continue to explore various topics related to Semantic Search as well as Search and Ranking in general over the next few weeks.
If you like learning about these types of concepts, don’t forget to subscribe to my blog below to get notified right away when there is a new post 🙂 Have an amazing week ahead!