Category: Bit Manipulation

n & (n -1) is a pretty powerful bitwise operation and we will see why in this post.

Power of two

Given an integer, we have to write a function to determine if it is a power of two.

Examples:

Input: 1
Output: true
Explanation: 2⁰ = 1

Input: 32
Output: true
Explanation: 2⁵ = 32

Input: 100
Output: false

What do powers of two look like in binary representation?

• 1 – 1
• 2 – 10
• 4 – 100
• 16 – 1000
• 32 – 10000

Notice that the integers above have only one 1-bit followed by all zeroes.

When we subtract 1 from any number, the rightmost 1-bit gets set to 0 and all the bits following this rightmost 1-bit will be set to 1. Let’s look at a few examples. In binary subtraction, when we perform 0 – 1, the result is 1 with a borrow of 1 from the next higher order bit. Borrowing can be tricky, here is good video that goes over binary subtraction.

When we AND the results above with the original integers, the result is 0. To conclude, if n & (n – 1) equals zero, then the given integer is a power of two. Other numbers have more than one 1-bit in the binary representation, so this trick will not return zero for those cases.

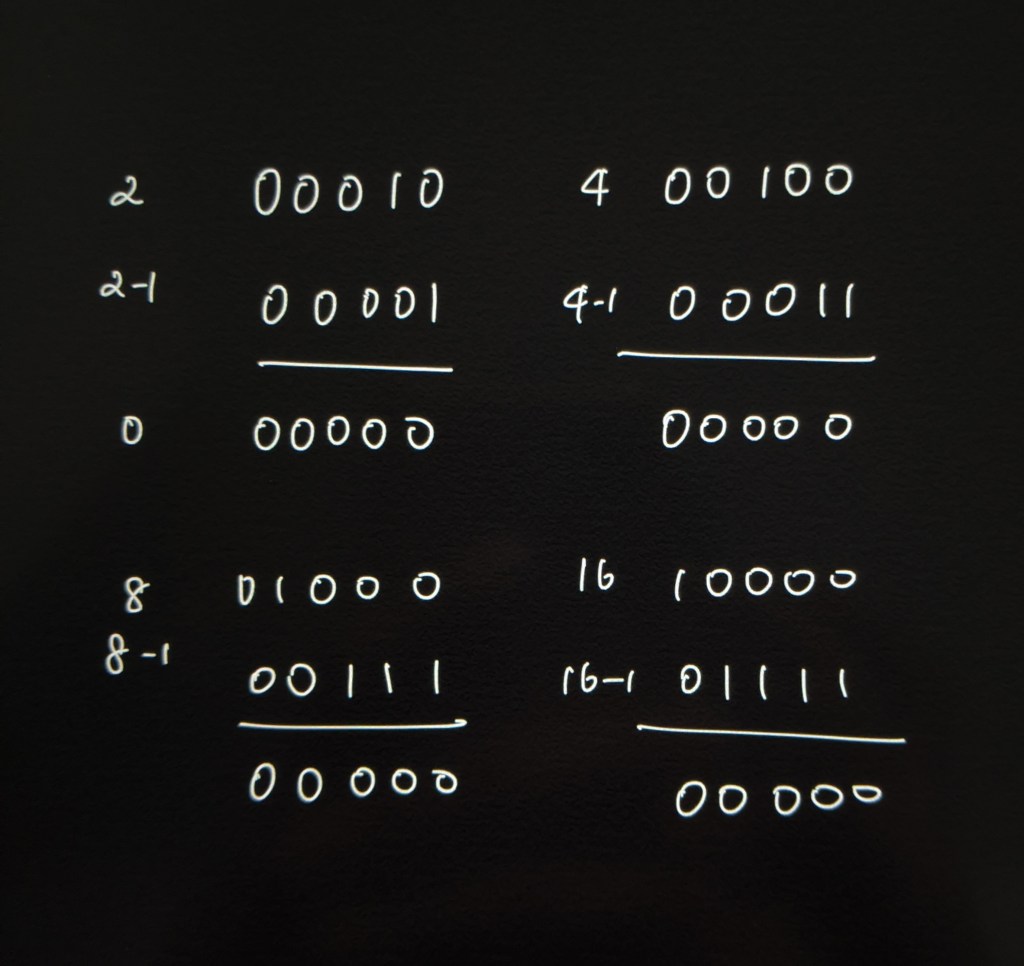
Time Complexity: O(1)

Space Complexity: O(1)

Code:

def isPowerOfTwo(self, n: int) -> bool:

    if n == 0:
        return False
    return n & (n-1) == 0

Count the number of ones in an unsigned integer

Essentially what n & (n-1) does is that it sets the right most 1-bit in an integer to 0. If we do that repeatedly, at some point all the bits get set to 0. We can use this same expression to count the number of one bits in any given unsigned integer without having to count the ones by traversing bit by bit. The number of 1-bits in an integer is also known as the hamming weight of a number.

Time Complexity: An unsigned integer will be 4 bytes ie., 32 bits long at maximum. The worst case happens when all the bits of an integer are 1 and we have to loop through it 32 times setting the rightmost bits to 0. If we consider this to be a constant time operation since an integer can never have more than 32 bits, then the time complexity will be O(1).

Space Complexity: O(1)

Code:

def hammingWeight(self, n: int) -> int:

    count = 0

    while n:
        n &= n-1
        count += 1

    return count
        

Hope you had fun learning this useful bit manipulation trick. Have a nice day!