Today’s problem is a very interesting one but is usually worded poorly in most places.
We are given an array W of positive integers where W[i] refers to the weight of index i. We have to write a function called pickIndex which will randomly pick an index proportional to its weight. Let’s look at an example to understand this better.
W = [1, 2, 3, 4, 5]
In the above case the weights are as follows.
W[0] = 1
W[1] = 2
W[2] = 3
W[3] = 4
W[4] = 5
How do we randomly pick an index proportional to its weight?
The weights of all the indexes in the array sum to 15 (1 + 2 + 3 + 4 + 5).
For index i = 0 with weight = 1, we have to pick this index once out of 15 times
For index i = 4 with weight = 5, we have to pick this index five out of 15 times
The bottomline line is that the indexes with the higher weights should have high probability of being picked, in this case that probability is:
P(i) = W[i] / sum(W)
ie., for index = 4 P(4) = 5/ 15 = 1/ 3.
Solution #1:
For probability problems, one of the foremost things we need is a sample space. Let’s simulate this using a generated array with 15 entries where each entry corresponds to an index in the array and appears W[i] number of times. For example, the index 4 should appear W[4] = 5 times in the array.
Sample space = [0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4]
If we are to pick a number randomly from the above list, we have solved the problem of picking a random index proportional to its weight.
Time Complexity: The time complexity will be O(sum(W)) to generate the sample space array.
Space Complexity: The simulated array will cost us O(sum(W)) extra space.
Code for solution #1:
class Solution(object):
def __init__(self, w: List[int):
totalSum = sum(w)
table = [0] * totalSum
i = 0
for j in range(0, len(w)):
for k in range(i, i + w[j]):
table[k] = j
i = i + w[j]
self.size = len(table)
self.table = table
def pickIndex(self) -> int:
randomIdx = random.randint(0, self.size - 1)
return self.table[randomIdx]
# Your Solution object will be instantiated and called as such:
obj = Solution(w)
param_1 = obj.pickIndex()
The above solution is extremely memory intensive since we generate an array that’s mostly larger than the input array itself to simulate the sample space.
Solution #2:
The total sum of our weights sum(W) is 15. If we had to draw a line and divide it according to the given weights ranging from 1 to 15, how would that look like?
W = [1, 2, 3, 4, 5]
sample_space = [0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4]

Instead of generating an entirely new array with the repeated indexes, we can calculate the prefix sums for each index. The formula to find the prefix sum of W[i] is shown below.
W[i] = W[i] + W[i-1]
Then our prefix array will look like this.
W = [1, 3, 6, 10, 15]
The total weight 15 is the length of our sample space. We will first generate a random number between 1 and 15.
randIndex = random.randint(1, maxWeight)
Let’s say that the randIndex returns 8. This index falls in the range (6 – 10]. So we return the index filling up this range which is 3.
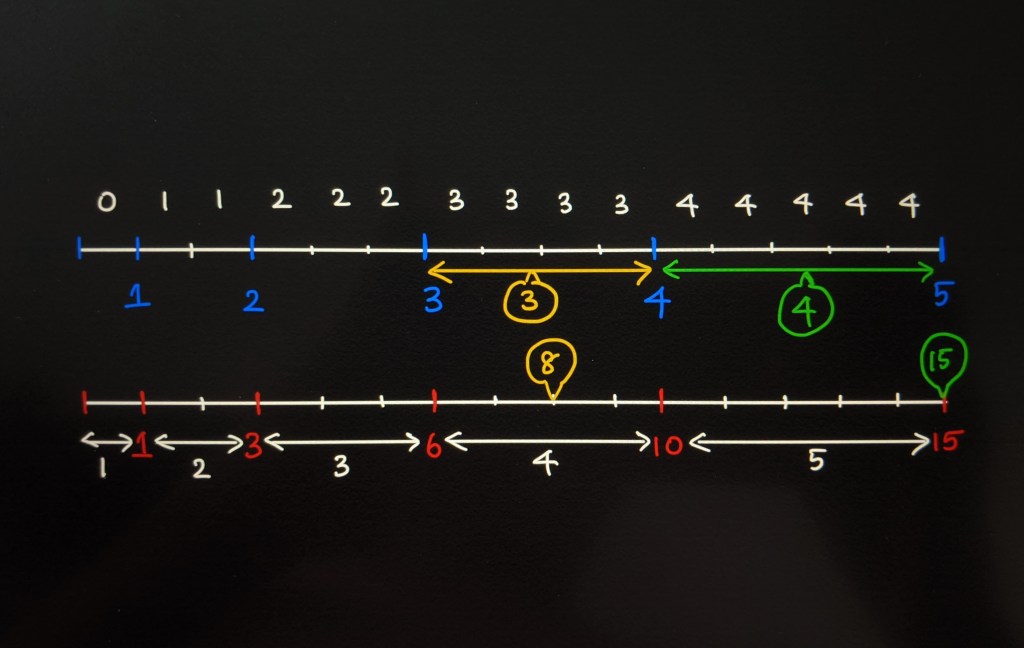
If the randIndex returns 15, this number falls in the range (10 – 15]. So we return the index filling up this range which is 4.
We find this range using linear search on the prefix sum W array. All we have to find a value such that value <= randIndex which indicates that it has fallen in that particular range. In that case, we return the index of this value.
Time Complexity: O(N) to calculate prefix sum and O(N) to find the randIndex value in the prefix sum array. This means the pickIndex function call runs in O(N) time.
Space Complexity: O(1) since we are not using any extra space.
Code for solution #2:
class Solution:
def __init__(self, w: List[int]):
# Calculate the prefix sums
w = list(itertools.accumulate(w))
self.w = w
if self.w:
self.maxWeight = self.w[-1]
else:
self.maxWeight = 0
def pickIndex(self) -> int:
randIndex = random.randint(1, self.maxWeight)
for i, prefixSum in enumerate(self.w):
if randIndex <= prefixSum:
return i
return 0
#Your Solution object will be instantiated and called as such:
obj = Solution(w)
param_1 = obj.pickIndex()
Solution #3:
In the above solution pickIndex() runs in O(N) time and it’s basically doing a linear search in the array to find the range of the randIndex. We can improve the time complexity using binary search.
In the binary search algorithm, if our randIndex value matches an entry in the prefix sums array, we return that index. Else we return the index of a value which is <= randIndex. This is basically a binary search to find a number N such that N <= target.
Time Complexity: O(logN) to pick the index.
Space Complexity: O(1)
Code for solution #3:
class Solution(object):
def __init__(self, w: List[int]):
w = list(itertools.accumulate(w))
self.w = w
if self.w:
self.maxWeight = self.w[-1]
else:
self.maxWeight = 0
def pickIndex(self) -> int:
randIndex = random.randint(1, self.maxWeight)
# Binary search for randIndex
left = 0
right = len(self.w) - 1
while left <= right:
mid = (left + right) / 2
if self.w[mid] == randIndex:
return mid
if self.w[mid] < randIndex:
left = mid + 1
else:
right = mid - 1
return left
# Your Solution object will be instantiated and called as such:
obj = Solution(w)
param_1 = obj.pickIndex()
Solution #4 (Optional):
The code in solution #3 can be written in a very pythonic way using built-in functions as shown below. The time and space complexity will be the same.
Python’s bisect.bisect_left() returns an insertion point i that partitions the array into two halves such that all(val < randIndex for val in w[left : i]) for the left side and all(val >= randIndex for val in a[i : right]) for the right side. Read more here.
class Solution:
def __init__(self, w: List[int]):
self.w = list(itertools.accumulate(w))
def pickIndex(self) -> int:
return bisect.bisect_left(self.w, random.randint(1, self.w[-1]))
#Your Solution object will be instantiated and called as such:
obj = Solution(w)
param_1 = obj.pickIndex()
Hope you learnt to methodically approach the random pick with weight problem. Have a nice day!